Hostname: page-component-8448b6f56d-m8qmq Total loading time: 0 Render date: 2024-04-24T23:46:44.088Z Has data issue: false hasContentIssue false
  • English
  • Français

Algebraic Properties of a Family of Generalized Laguerre Polynomials

Published online by Cambridge University Press:  20 November 2018

Farshid Hajir
Farshid Hajir*
Affiliation:
Department of Mathematics & Statistics, University of Massachusetts, Amherst, Amherst MA 01003, USA, hajir@math.umass.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

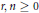We study the algebraic properties of Generalized Laguerre Polynomials for negative integral values of the parameter. For integers $r,n\ge 0$, we conjecture that 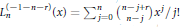$L_{n}^{(-1-n-r)}(x)=\Sigma _{j=0}^{n}\left( _{n-j}^{n-j+r} \right){{x}^{j}}/j!$ is a 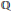$\mathbb{Q}$-irreducible polynomial whose Galois group contains the alternating group on $n$ letters. That this is so for 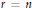$r=n$ was conjectured in the 1950's by Grosswald and proven recently by Filaseta and Trifonov. It follows fromrecent work of Hajir and Wong that the conjecture is true when $r$ is large with respect to 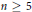$n\ge 5$. Here we verify it in three situations: (i) when $n$ is large with respect to $r$, (ii) when 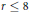$r\le 8$, and (iii) when 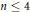$n\le 4$. The main tool is the theory of $p$-adic Newton Polygons.

Keywords

11R0905E35
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 3 , 01 June 2009 , pp. 583 - 603
Copyright
Copyright © Canadian Mathematical Society 2009

References

[A] Amice, Y., Les nombres p-adiques. Collection SUP: Le Mathèmaticien 14, Presses Universitaires de France, Paris, 1975.Google Scholar
[AAR] Andrews, G. E., Askey, R., and Roy, R., Special functions. Encyclopedia of Mathematics and its Applications 71, Cambridge University Press, Cambridge, 1999.Google Scholar
[Ar] Artin, E., Algebraic numbers and algebraic functions. Gordon and Breach Science Publishers, New York-London-Paris, 1967.Google Scholar
[B] Batut, C., Belabas, K., Bernardi, D., Cohen, H., and Olivier, M., GP-PARI 2.0.12, http://pari.math.u-bordeaux.frGoogle Scholar
[C] Coleman, R. F., On the Galois groups of the exponential Taylor polynomials. Enseign. Math. (2)). 33(1987), no. 3-4, 183–189.Google Scholar
[D] Dumas, G., Sur quelques cas d’irrèducibilitè des polynomes à coefficients rationnels. J. de Math. Pures et Appl. 2(1906), 191–258.Google Scholar
[F] Feit, W., ˜A5 and ˜A7 are Galois groups over number fields. J. Algebra 104(1986), no. 2, 231–260.Google Scholar
[F1] Zelenyuk, Y., On the irreducibility of all but finitely many Bessel polynomials. Acta Math. 174(1995), no. 2, 383–397.Google Scholar
[F2] Zelenyuk, Y., A generalization of an irreducibility theorem of I. Schur. In: Analytic number theory 1, Progr. Math. 138, Birkhäuser Boston, Boston, MA, 1996, pp. 371–396.Google Scholar
[FL] Filaseta, M. and Lam, T.-Y., On the irreducibility of the generalized Laguerre polynomials. Acta Arith. 105(2002), no. 2, 177–182.Google Scholar
[FT] Filaseta, M. and Trifonov, O., The irreducibility of the Bessel polynomials. J. Reine Angew. Math. 550(2002), 125–140.Google Scholar
[FW] Filaseta, M. and Williams, R. L., Jr., On the irreducibility of a certain class of Laguerre polynomials. J. Number Theor. 100(2003), no. 2, 229–250.Google Scholar
[G] Gouv, F. Q.êa, p-adic numbers. An introduction. Second edition, Springer-Verlag, Berlin, 1997.Google Scholar
[Go] Gow, R., Some generalized Laguerre polynomials whose Galois groups are the Alternating groups. J. Number Theor. 31(1989), no. 2, 201–207.Google Scholar
[Gr] Grosswald, E., Bessel polynomials. Lecture Notes in Mathematics 698, Springer, Berlin, 1978.Google Scholar
[H1] Hajir, F., Some A˜n-extensions obtained from generalized Laguerre polynomials. J. Number Theory 50(1995), no. 2, 206–212.Google Scholar
[H2] Hajir, F., On the Galois group of generalized Laguerre Polynomials. J. Thèor. Nombres Bordeau. 17(2005), no. 2, 517–525.Google Scholar
[HW] Hajir, F. and S.Wong, Specializations of one-parameter families of polynomials. Ann. Inst. Fourier (Grenoble). 56(2006), no. 4, 1127–163.Google Scholar
[HK] Harborth, H. and Kemnitz, A., Calculations for Bertrand's postulate. Math. Mag. 54(1981), no. 1, 33–34.Google Scholar
[Ha] Hasse, H., Number theory. Classics in Mathematics, Springer-Verlag, Berlin, 2002.Google Scholar
[HL] Hensel, K. and Landsberg, G., Theorie der algebraischen Funktionen einer Variabeln und ihre Anwendung auf algebraische Kurven und Abelsche Integrale. Chelsea Publishing Co., New York, 1965.Google Scholar
[ M] Mott, J. L., Eisenstein-type irreducibility criteria. In: Zero-dimensional commutative rings, Lecture Notes in Pure and Appl. Math. 171, Dekker, New York, 1995, pp. 307–329.Google Scholar
[PRT] Pacetti, A., Rodriguez-Villegas, F., and Tornaria, G., Computational Number Theory Tables and Computations, http://www.ma.utexas.edu/users/tornaria/cnt/.Google Scholar
[PZ] Pólya, G. and Szegʺo, G., Problems and theorems in analysis. Vol. II. Theory of functions, zeros, polynomials, determinants, number theory, geometry. Die Grundlehren der Mathematischen Wissenschaften 216, Springer-Verlag, New York, 1976.Google Scholar
[RS] Rosser, J. B. and Schoenfeld, L., Approximate formulas for some functions of prime numbers. Illinois J. Math. 6(1962), 64–94.Google Scholar
[Sc1] Schur, I., Gleichungen Ohne Affekt. In: Gesammelte Abhandlungen. Band III, Springer-Verlag, Berlin, 1973, pp. 191–197.Google Scholar
[Sc2] Schur, I., Affektlose Gleichungen in der Theorie der Laguerreschen und Hermiteschen Polynome. In: Gesammelte Abhandlungen. Band III, Springer-Verlag, Berlin-New York, 1973, pp. 227–233.Google Scholar
[S] Sell, E. A., On a certain family of generalized Laguerre polynomials. J. Number Theor. 107(2004), no. 2, 266–281.Google Scholar
[Se] Serre, J.-P., L’invariant de Witt de la forme Tr(x2). Comment. Math. Helv). 59(1984), no. 4, 651–676.Google Scholar
[Sz] Szegʺo, G., Orthogonal polynomials. Fourth edition, American Mathematical Society, Providence, RI, 1975.Google Scholar